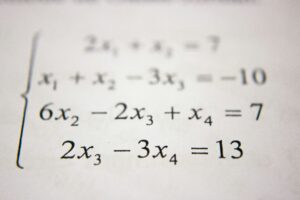
Parallel Practice is a new column exploring the other practices and disciplines that inform but are separate from our writing practice. The essays highlight how the other things we choose to do with our single, precious lives allow us to think expansively, take risks, pursue technical excellence, show up for ourselves, and everything else that goes into generative work.
***
Words often failed me as a child. I might blame my terse relatives, who had a vocabulary for their industries but none they readily shared for art or beauty or love. The truth is, English was not always equal to my thoughts. Whereof I could not speak I remained silent, and there was so much space available for my silence.
Beyond words, perhaps orthogonal to them, I located numbers. I could not conjure the grace of a left-handed swing, but I could calculate a batting average, well beyond the usual decimals, at seven years old. I was too shy ever to boast of winning a footrace, but I knew my average speed owing to the distance and time that I ran. I could scarcely analyze the books I read, but I knew the formula to every number of the near-infinite series of Hardy Boys novels. I could not always count on my friends, but I could enumerate their slights.
Beyond numbers, in truth exceeding them, I located mathematics. Its terms revealed an organizational structure that made sense of the world, finally, to my methodical mind. People and their intentions were shifty; mathematics was not. Addition, I learned, perhaps too early, was absolute; 2+2=4, everywhere and anywhere, now and then and forever. This was a necessary truth of the universe that neither parents nor politics could rewrite (thus the irony of 1984).
Yet math was not some hidebound pursuit, its rules no mere strictures. They were the creative limitations that set me free. Math would be the precise stability, the fundamental reality, I needed to gird and enrich my inner life.
In grade school, I learned the times table so quickly that my teacher would not let me compete against the other students in daily drills. I did not truly realize how adept I was at mathematics, however, until the seventh grade. After the first week of classes, the teacher handed me an algebra book and told me to sit in the hall with another student and study on my own.
I crushed on that student, I now realize, the first person who recognized the fecundity of math as I did, who met me intellectually. But I kept my distance for almost two semesters. I preferred the illusion of self-control to my reckless emotions. We traded only answers, that student and I, because no words could have equaled our love for that new math.
An alphabet had invaded the equations of algebra but only to embody the world’s mysteries. Letters were turned to symbols for the ineffable, like astrological signs or runes. Algebra was no mere symbology, however. It was the manipulation of symbols, of lines and figures, toward resolute ends. It was a true numerology, a reliable yet effable magic. I coveted its tricks.
I learned math as most people do, as a series of problems requiring solutions. In the original lessons, there was only ever one or two answers to any question. I believed that math thus belied the solutions to all problems, not just my own. It was not only a bulwark but a decision tree. It was how I might navigate, if not know, the wider world.
By high school I learned there was, most often, an infinite number of solutions to even the simplest problems. Other times there were none. The best I might hope for was thus a surfeit of information or a humble approximation to what I wanted to know. And that was before I learned about inequalities.
Even when I could resolve every solution to a problem, what did such knowledge afford? Which was the most apt solution, the one I should pursue? To the math it did not matter. One answer was tantamount to another. To me, it meant the world.
I had always wanted to calculate without becoming calculating, but math did not permit the desiderata I wished for. In fact, little was resolved by my formulas beyond the simplest knowledge I sought. I suppose I could have been repulsed or unmotivated by my ignorance. I was entranced. Whereof no one knew, I might finally speak.
Real mathematics is neither addition nor subtraction, neither multiplication nor division, just as writing goes beyond proper spelling and art is more than a brush with paint.
In calculus, we learn what is integral, what is derivative. We reach for limits and nudge infinity. We represent motion as infinitesimal steps along endless, winding paths.
We have no direct experience with such infinities, whether they be big or small. They are each abstract, if not wholly unreal. Even the horizon or an ocean view, even a peep into the expanse of the universe, are not vistas unto any real infinity.
We are finite beings confined by our limited time and space on Earth. We must reason with infinity much as we do with every other boundless abstraction, such as freedom and justice and love. Through metaphors. We seek analogies equal to, if not firmer than, our vague experiences and thoughts. In mathematics, such metaphors are often identical to the ones we employ in language because they both originate in what we experience, in what we can know. Infinity is but an analogy we build from all we cannot see.
Mathematics does not reduce the world to numbers. It expands what we observe to encompass the numerics already imbued everywhere in everything. It reveals the patterns that naturally emerge from the great disorder of our lives.
Math comes from warm bodies, even when those bodies pursue cold, objective truths. In other words, we create meaning with equations just as we do with words.
Throughout college, I acquired the orthography of mathematics and internalized its grammars, although I largely spoke its humble dialect, theoretical physics. I was a polyglot, and mathematics, I explained to people unoriginally, was but another foreign language. It encoded different experiences. It allowed varying descriptions of the world. It resounded with its own lilt and poetry. We need not be beholden to any one collection of words or any one deck of symbols to understand the universe and describe it. Math, too, offered us its allusions and convictions. Math, too, leavened our souls.
The primary object of calculus is the function, usually abbreviated f(x). Teachers describe it as a machine—one input leading relentlessly to an output. I never understood it as such.
A function, to me, was a connection between two or more entities or ideas, usually one we knew and one we did not. We called those entities variables because we allowed them, and what they stood for, to change. One variable, x, might depend on another, y, because the one changed as the other did. Calculus was nothing but a survey of such relationships, especially as they developed across distance or time.
Relationships were so central to the enterprise that mathematicians gathered everything, even the most basic numbers, into groups or families with shared traits. Some were complex. Others negative or irrational. A few were imaginary or hyperreal.
Such categories were comforting to me, especially when other categories were not. Every group of numbers had a well-defined identity. But math also revealed the similarities across any external differences. It detailed the varieties of numeric kin. Two could be equivalent to four and even to six, in certain number systems. Primes were numbers from which all the integers had multiplied. A donut was the same as a coffee mug, at least to a topologist who cared only about holes. Our friendships, our social networks, were but connected graphs, links in abstract webs, with finite degrees of separation.
The greatest splendor of math was eventually revealed to me, however, in just how much of it and its associations were imaginary. In how much of the unreal codified the real. How fiction was necessary to understand the nonfiction world. To understand the attractions and repulsions of electrons, to feel their true currents and shocks, for example, required imaginary numbers. In fact, math’s fictions not only represented aspects of this world, they applied to any possible one. Math’s realism was surreal.
One afternoon while writing this essay, I opened Don Delillo’s minor novel about mathematics, Ratner’s Star, which I had read shortly after I decided to become a writer rather than a theoretical physicist. I saw this absurd truth: “Existence would be sheer dread without the verifiable fictions of mathematics.”
Math humbled me in graduate school, but it also soothed and restrained me. I calculated in longhand, preferring mechanical pencils and Japanese paper on which the lead squeaked but did not smear. Forced to write slower than the speed of my thoughts, my mind did not wander so much as sharpen to my task. Calculating was the most effective antianxiety medicine I took, focusing me on the more immediate problems of math.
Pure mathematics is often the work of tidying up or making arrangements, because solving equations usually leads to a mess. Tangles of terms will proliferate and obscure an equation’s sense, just as clauses do a run-on sentence. The chore is to simplify, to combine terms and join ideas into their clearest expressions. To emend the extraneous without ruining the correspondence between what we do and do not know.
As my calculations increased in size, I learned to manage the task of deriving solutions in parts without losing the plot. I rearranged segments of texts constantly, looking for ways to join and redact them. I balanced negative signs against positive ones, looked for resonances between different terms, focused on the intricate details of sub- and superscripts, anticipated surprises or twists, reveled in graphic imagery, contemplated next steps.
My penmanship, like that of most who dabbled with math, was often exquisite. Sometimes, the math looked so beautiful that it had to be right. Beauty had rendered truth. Most times, however, I would write myself into a corner and have to start over, no matter how beautiful the math. I had to find a new way forward, even if it required an uglier or more tangled pursuit. I had to hope some unseen clearing or climax would reveal itself when I did not know how to proceed. Oftentimes, it did not.
Math was a sedentary activity, one I usually did in a La-Z-Boy or a café. But the surest tactic to proceed on a difficult problem was a cliché —to leave my calculations behind and go for a walk. To give in to the subconscious with a change of scene. To wander with my mind through unknowing, until we discovered some hidden but clear path by which to proceed, by which to create sense.
I knew it was time to quit doing math professionally when I was in excellent shape. When all I did was walk. Yet math continues to rouse me, even to calm me. Numbers especially remain a solace.
I still count my breaths and steps as I run, and I do not take any leap until in my head I reach the number three, just as I did when I was a kid. A chain link fence is but a rotated graph on which I still like to imagine curves and plots. I classify shapes by their topologies, exploit theories even in friendly games. I still find beauty in primes. I optimize, classify, and organize problems to hunt for solutions, as I once did in lines of math. I see the tensors in tensile objects, the self-similarity in leaves and trees, the links in my web of friendships, the geometries embedded within music and art.
Every morning, for almost two decades, I have continued to check ArXiv.org, a repository for the latest articles about physics and math. So thorough is my devotion to what adherents call “the archive” that I often perform this rite before I have had my coffee, which I have made for myself out of necessity every morning since I was fourteen. I still look to math and its related theories, to navigate, if not know, the greater world.
I recently moved from Austin to Los Angeles, which not only meant downsizing to a smaller place but scuppering the detritus of my former life. For the first time since the birth of my child, I had to decide what was truly important. I discarded clothes, shoes, stories, art, and friends. I discarded drafts of the book that I have been writing far longer than anyone should—a number of years in the double digits. I know too well how much I have yet to show the world. Yet, I kept all eight boxes that I have of my apprentice math as a necessary balm.
I know that math does not make sense of the entire universe. That it never will. I also know that it does conform to many pieces of the universe remarkably well. This is often all I need from it. To make sense of some immediate piece. To ease the ache of existence.
As when my child was in the hospital for several days with a lump in the neck, when we did not yet know if it was cancerous, when I started to count and then calculate mindlessly. Drips of saline. Beeps of monitors. Vials of blood. Hours awake. Volumes of medicines, in containers of various shapes. Efficacy of doses. Rates of mortality. I was seeking comfort in what numbers could tell me, because I feared what they could not.
Utility precedes aesthetics. This is the case in both language and math. Humans developed and retained words and numbers, foremost, because they were useful. They expressed our ideas and needs and emotions better than violence and grunts. Prosody lagged. But rhythm brought to language and math what is most profound. The abstractions by which we survive.
Henry David Thoreau once wrote: “We have heard about the poetry of mathematics, but very little of it has yet been sung.”
I am now, as I was as a child, often inarticulate about my emotions and needs. But I have always wanted to sing.
I realize now that I have often tried to reveal something of the rhythm of mathematics, something of its pulse and allure, to those I love, awkwardly, in moments of intimacy. I wanted to match one vital abstraction to another, much as I did with my classmate in the seventh grade.
One of the final times I visited home from college, before I left for good, I walked into the kitchen in the early morning and found my sister, who was then my best friend. I felt the sudden necessity to tell her I loved her. On a napkin, instead, I giddily explained infinity and calculus, and their relationships to change. I filled fold after fold with meticulous curves and geometries. I told her about math’s visual arts while she spoke to me about painting, sharing her abstract passion with me.
I can count on two hands the number of times my father has called me, but almost every one of those times his excuse for connection was a problem in math. The time he asked me to correct an errant algorithm he had developed for work. The time he called, when layoffs were imminent, to devise a formula that might reduce the inefficiencies of his company’s production line. He wanted to know an output for any input. The function I developed did not solve the company’s problem, because none could.
My father never progressed beyond algebra in high school. His knowledge of math was largely self-taught. I later realized that in helping my dad, I had been trying to derive an expression equal to my love for him. When I could not, I wanted him to experience math’s poetry and magic as I did, not merely its utility.
That Christmas, I bought him a book, Calculus Made Easy. In one of the eight boxes of my juvenile math, which Dad had lacquered with tape and later shipped to me through the mail, I found my gift to him, still with perfect posture. Its spine uncracked, its contents unread.
You can deprive yourself of math, much as you can deplore music or dance or art. But I do not revel in any impoverishment. I will never doubt what math has given me.
On the winter morning when I fell in love with the woman who swells my life still, we sat vulnerable in bed with the schemes of econometrics beside us. We did calculations that made sense of the machinations of financial systems and of entire governments though not our relentless attraction, not where our paths had crossed and refused to diverge.
When my child finally recovered and left the cancer ward this past summer, I started to pass on the grammar of a deeper love. I wanted to embrace him with something universal and true and beautiful.
I began to teach him addition, for whenever words failed.
***
Artwork by Antoine Dautry




